Ας είναι τυχών – διάστατος διανυσματικός χώρος πάνω στο σώμα των πραγματικών αριθμών .
Ορισμός 1. Μια απεικόνιση ονομάζεται εσωτερικός πολλαπλασιασμός, όταν ισχύουν οι εξής ιδιότητες:
a) ,
b) ,
c) ,
d)
![]() ,
, ![]()
e)
![]() .
.
Ορισμός 2. Ο αριθμός ![]() ονομάζεται εσωτερικό γινόμενο
των διανυσμάτων
ονομάζεται εσωτερικό γινόμενο
των διανυσμάτων ![]() .
.
Ορισμός 3. Ο μη αρνητικός αριθμός ![]() ονομάζεται μέτρο του
διανύσματος
ονομάζεται μέτρο του
διανύσματος ![]() και συμβολίζεται
και συμβολίζεται ![]() . Χρησιμοποιούμε επίσης το σύμβολο
. Χρησιμοποιούμε επίσης το σύμβολο ![]() .
.
Ορισμός 4. Κάθε διανυσματικός χώρος στον οποίο έχει οριστεί ένας εσωτερικός πολλαπλασιασμός ονομάζεται ευκλείδειος διανυσματικός χώρος.
Ορισμός 5. Δύο διανύσματα ![]() ενός ευκλείδειου
διανυσματικού χώρου
ενός ευκλείδειου
διανυσματικού χώρου ![]() ονομάζονται κάθετα (
ονομάζονται κάθετα (![]() ) ακριβώς τότε, όταν
) ακριβώς τότε, όταν ![]() .
.
Προφανώς ο ορισμός αυτός δεν αποκλείει τις
περιπτώσεις ένα από τα δύο διανύσματα ή και τα δύο να είναι μηδενικά, αφού ![]() ,
, ![]() .
.
Πράγματι, ισχύει ![]() ,
, ![]() και με χρήση της
ιδιότητας (c) του oρισμού 1, προκύπτει
και με χρήση της
ιδιότητας (c) του oρισμού 1, προκύπτει ![]() . Έτσι:
. Έτσι:
Το
μηδενικό διάνυσμα του ![]() θεωρείται κάθετο σε
κάθε διάνυσμα αυτού.
θεωρείται κάθετο σε
κάθε διάνυσμα αυτού.
Ορισμός 6. Μια βάση ![]() ενός ευκλείδειου
διανυσματικού χώρου
ενός ευκλείδειου
διανυσματικού χώρου ![]() ονομάζεται ορθομοναδιαία ή ορθοκανονική, όταν ισχύει
ονομάζεται ορθομοναδιαία ή ορθοκανονική, όταν ισχύει
(1.1) ![]() ,
, ![]() ,
,
όπου
![]()
είναι το σύμβολο του Kronecker.
Λέμε, ισοδύναμα, ότι η ![]() είναι ορθομοναδιαία
ακριβώς τότε, όταν τα διανύσματά της είναι κάθετα ανά δύο και έχουν μέτρο
μονάδα (μοναδιαία
διανύσματα).
είναι ορθομοναδιαία
ακριβώς τότε, όταν τα διανύσματά της είναι κάθετα ανά δύο και έχουν μέτρο
μονάδα (μοναδιαία
διανύσματα).
Παρατήρηση 1. Ο ορισμός του εσωτερικού γινομένου δόθηκε χωρίς τη
χρήση βάσης του ![]() , άρα δεν εξαρτάται από την επιλογή της.
, άρα δεν εξαρτάται από την επιλογή της.
Ας θεωρήσουμε τώρα τυχούσα βάση ![]() ενός ευκλείδειου διανυσματικού
χώρου
ενός ευκλείδειου διανυσματικού
χώρου ![]() . Για δύο τυχόντα διανύσματα
. Για δύο τυχόντα διανύσματα ![]() υπάρχουν μοναδικά
υπάρχουν μοναδικά
![]() ,
, ![]() , έτσι ώστε
, έτσι ώστε ![]() και
και ![]() . Χρησιμοποιώντας τις ιδιότητες του εσωτερικού πολλαπλασιασμού
βρίσκουμε
. Χρησιμοποιώντας τις ιδιότητες του εσωτερικού πολλαπλασιασμού
βρίσκουμε
(1.2) ![]()
και, αν θέσουμε ![]() στην (1.2),
στην (1.2),
(1.3) 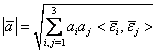 .
.
Ώστε, το εσωτερικό γινόμενο δύο
διανυσμάτων και το μέτρο ενός διανύσματος υπολογίζονται, όταν γνωρίζουμε τα
εσωτερικά γινόμενα των διανυσμάτων της βάσης ![]() .
.
(1.4) ![]() ,
,
(1.5) ![]() .
.
Παρατήρηση 2. Σ’ ένα διδιάστατο διανυσματικό χώρο ![]() οι τύποι για το
εσωτερικό γινόμενο δύο διανυσμάτων
οι τύποι για το
εσωτερικό γινόμενο δύο διανυσμάτων ![]() και το μέτρο
ενός διανύσματος
και το μέτρο
ενός διανύσματος ![]() , ως προς ορθομοναδιαία βάση
, ως προς ορθομοναδιαία βάση ![]() , γίνονται αντίστοιχα
, γίνονται αντίστοιχα
![]() ,
,
![]() .
.
Παράδειγμα 1. Ας είναι ![]() ορθομοναδιαία βάση
ενός διδιάστατου ευκλείδειου διανυσματικού χώρου
ορθομοναδιαία βάση
ενός διδιάστατου ευκλείδειου διανυσματικού χώρου ![]() και
και ![]() ,
, ![]() δύο διανύσματα του
δύο διανύσματα του ![]() με συντεταγμένες ως
προς τη βάση
με συντεταγμένες ως
προς τη βάση ![]() . Σύμφωνα με την παρατήρηση 2 το εσωτερικό γινόμενο των
. Σύμφωνα με την παρατήρηση 2 το εσωτερικό γινόμενο των ![]() είναι
είναι
(1.6) ![]() .
.
και τα μέτρα τους
(1.7) ![]()
![]()
![]() ,
, ![]() .
.
Παράδειγμα 2.
Σ’ ένα τρισδιάστατο ευκλείδειο διανυσματικό χώρο ![]() δίνεται ορθομοναδιαία
βάση
δίνεται ορθομοναδιαία
βάση ![]() και το διάνυσμα
και το διάνυσμα ![]() . Να βρεθεί μοναδιαίο διάνυσμα
. Να βρεθεί μοναδιαίο διάνυσμα ![]() κάθετο στο
κάθετο στο ![]() .
.
Λύση. Ας είναι ![]() οι συντεταγμένες του
διανύσματος
οι συντεταγμένες του
διανύσματος ![]() ως προς τη βάση
ως προς τη βάση ![]() . Τα διανύσματα
. Τα διανύσματα ![]() ,
,![]() είναι κάθετα ακριβώς τότε, όταν
είναι κάθετα ακριβώς τότε, όταν ![]() . Εφαρμόζουμε τον τύπο (1.4) και βρίσκουμε
. Εφαρμόζουμε τον τύπο (1.4) και βρίσκουμε ![]() . Επομένως
. Επομένως
![]() ,
, ![]() .
.
Για κάθε πραγματική τιμή των ![]() ορίζεται ένα διάνυσμα
κάθετο στο
ορίζεται ένα διάνυσμα
κάθετο στο ![]() . Αν για παράδειγμα θεωρήσουμε
. Αν για παράδειγμα θεωρήσουμε ![]() και
και ![]() προκύπτει
προκύπτει ![]() για το οποίο, λόγω της
(1.5), ισχύει και
για το οποίο, λόγω της
(1.5), ισχύει και ![]() .
.
Γενικότερα, το διάνυσμα ![]() είναι μοναδιαίο, όταν
είναι μοναδιαίο, όταν ![]() ή ισοδύναμα, όταν
ή ισοδύναμα, όταν ![]() . Δηλαδή, πρέπει
. Δηλαδή, πρέπει ![]() . Άρα το σύνολο των ζητούμενων διανυσμάτων έχει τη μορφή
. Άρα το σύνολο των ζητούμενων διανυσμάτων έχει τη μορφή
![]() , όπου
, όπου ![]() .
.
Ορισμός 7. Ονομάζουμε γωνία δύο μη μηδενικών διανυσμάτων ![]() ενός ευκλείδειου
διανυσματικού χώρου
ενός ευκλείδειου
διανυσματικού χώρου ![]() τον αριθμό
τον αριθμό ![]() , για τον οποίο ισχύουν οι συνθήκες
, για τον οποίο ισχύουν οι συνθήκες
(1.8) 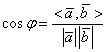 ,
, ![]() .
.
Προφανώς, όταν τα διανύσματα ![]() είναι
συγγραμμικά, η γωνία τους είναι 0 ή π.
είναι
συγγραμμικά, η γωνία τους είναι 0 ή π.
Παράδειγμα 3. Για τη γωνία ![]() των διανυσμάτων
των διανυσμάτων ![]() και
και ![]() του παραδείγματος 1
βρίσκουμε από τις σχέσεις (1.6), (1.7) και (1.8), ότι
του παραδείγματος 1
βρίσκουμε από τις σχέσεις (1.6), (1.7) και (1.8), ότι ![]() και
και ![]() , οπότε
, οπότε ![]() .
.
![]() Για τυχόντα διανύσματα
Για τυχόντα διανύσματα
![]() ενός ευκλείδειου
διανυσματικού χώρου
ενός ευκλείδειου
διανυσματικού χώρου ![]() ισχύουν:
ισχύουν:
(a) ![]() (ανισότητα Cauchy-Schwarz).
(ανισότητα Cauchy-Schwarz).
Η ισότητα ισχύει ακριβώς τότε,
όταν ![]() είναι γραμμικά
εξαρτημένα.
είναι γραμμικά
εξαρτημένα.
(b) ![]() (τριγωνικές
ανισότητες).
(τριγωνικές
ανισότητες).
Η ισότητα από αριστερά (αντ. δεξιά) ισχύει ακριβώς τότε,
όταν ![]() και
και ![]() (αντ.
(αντ. ![]() ).
).